2015-10-23
Below you will find annotated code and output related to the article “Issues in the Identification of Smoke in Hyperspectral Satellite Imagery—a Machine Learning Approach.” It is organized as follows:
The Expository Example
Two-predictor model
Expanding the feature space
A digression on principal components
Section 1 walks through a replication of the expository example of Section 2, where the green and blue channels of an RGB image are used to build a classifier. As a bonus an approach based on principal components is also demonstrated.
Section 2 gives an example not given in the chapter, still using RGB data. In this example all three channels, plus higher-order terms are included in the model. Model selection is performed and classifier building is done with separate training/test/validation data. This could be viewed as a “mini” version of the full analysis described in sections 3–5 of the chapter.
The short final section includes comments on scaling up the “mini” analysis to a full-blown one with large sets of megapixel hyperspectral images.
The files necessary to follow along with this analysis are contained in this zip file. It contains:
example_script.R, a script with all of the R code that appears on this page.helper_functions.R, a file with some utility functions I use but don’t document here, since they’re incidental to the main point.RGB.RData, a data file containing data frameRGBdata.
The Expository Example
Here is the image we will be using for the analysis. The red outlines surround areas that were determined to be smoke, and the blue rectangles indicate sub-images that will be used for the present analyses. In this expository example only the data from the sub-image at the center will be used, but for the extended example the data from both sub-images will be combined.
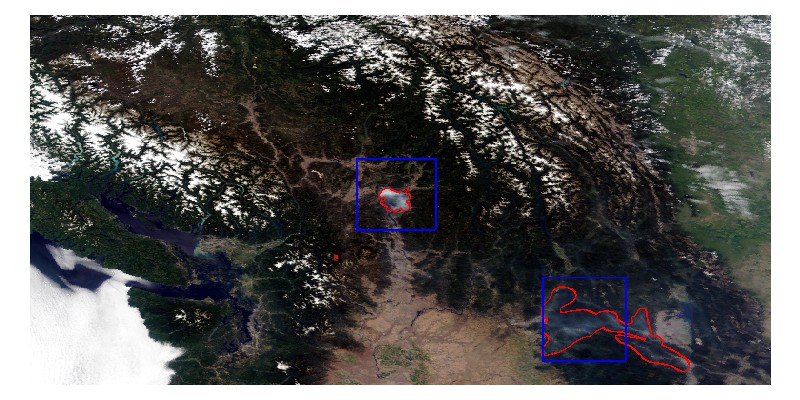
The data from all of the pixels in the two sub-images are found in the data frame RGBdata. It has four variables: class, R, G, and B. The class holds the true labels of the pixels (0 for nonsmoke, 1 for smoke), while the other three variables hold the color information (represented as numbers in [0,1]).
To begin we source helper_functions.R, load the data, and inspect it a little:
source("helper_functions.R") #-Load functions needed later.
load("RGB.RData") #-Loads data frame RGBdata.
dim(RGBdata)
head(RGBdata)Which gives output
> dim(RGBdata)
[1] 55375 4
> head(RGBdata)
class R G B
1 0 0.4000000 0.2941176 0.2313725
2 0 0.4000000 0.2941176 0.2313725
3 0 0.3882353 0.2862745 0.2235294
4 0 0.3882353 0.2862745 0.2235294
5 0 0.4078431 0.3176471 0.2588235
6 0 0.4078431 0.3176471 0.2588235Each of the 55375 rows in the data frame represents a pixel. The first 24750 rows hold data from the center sub-image (which is 150 by 165), and the remaining 30625 rows hold data from the lower-right sub-image (which is 175 by 175). In all, 14709 (or about 27%) of the pixels in the data set have true label smoke.
Two-predictor model
At present we are interested in a logistic regression model with only G and B as predictors, and using only the data from the first sub-image. This is done with
dat <- RGBdata[1:24750,] #-Data to use for this example.
smoke <- dat$class==1 #-For selecting only smoke pixels.
fit <- glm(class ~ G + B, family=binomial(link=logit), data=dat)
summary(fit)The summary command shows us the following:
Call:
glm(formula = class ~ G + B, family = binomial(link = logit),
data = dat)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.2675 -0.1065 -0.0590 -0.0390 3.2240
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -7.1813 0.1386 -51.80 <2e-16 ***
G -30.9704 1.0111 -30.63 <2e-16 ***
B 50.6900 1.1490 44.12 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 15322.2 on 24749 degrees of freedom
Residual deviance: 3559.9 on 24747 degrees of freedom
AIC: 3565.9
Number of Fisher Scoring iterations: 8which shows that both green and blue intensities have very large coefficients and, under this model, are highly statistically significant.
Perhaps more interesting is the plot of the data in (G,B) space, and the logistic model’s decision boundary. The code to produce the plot is shown below; the plot itself follows.
# Make the plot of the data points
windows(width=6, height=5)
par(cex=0.75, mar=c(5,4,0,2)+0.1, family="serif")
plot(dat$G[smoke], dat$B[smoke], xlim=c(0,1), ylim=c(0,1), pch=20, cex=0.25,
col="blue", xlab="Green", ylab="Blue")
points(dat$G[!smoke],dat$B[!smoke], pch=18, cex=0.25, col="red")
# Add the model's 50% probability contour line
ngrid <- 100
g <- b <- seq(0,1,length.out=ngrid)
pp <- function(g,b) predict(fit, newdata=data.frame(G=g,B=b), type="response")
z <- outer(g, b, pp)
levs <- 0.5
contour(g, b, z, levels=levs, add=TRUE, lwd=2)
# Add the image showing the predictions. Functions addoutline() and
# mask2outline() are for adding outlines to images, and are found in
# helper_functions.R. rImage() is also defined there. It's a small wrapper
# to the rasterImage() function of the graphics base package.
msk <- matrix(dat$class, nrow=150) #-Create "mask" matrix giving true labels.
FV <- matrix(fit$fitted.values, nrow=150) #-Fitted probabilities as an image.
FV <- addoutline(FV>0.5, mask2outline(msk, 2))
rImage(FV, c(0, 0.7, 0.33, 1))
text(0.165, 0.7, "model prediction\n(white = smoke)", pos=1, family="serif")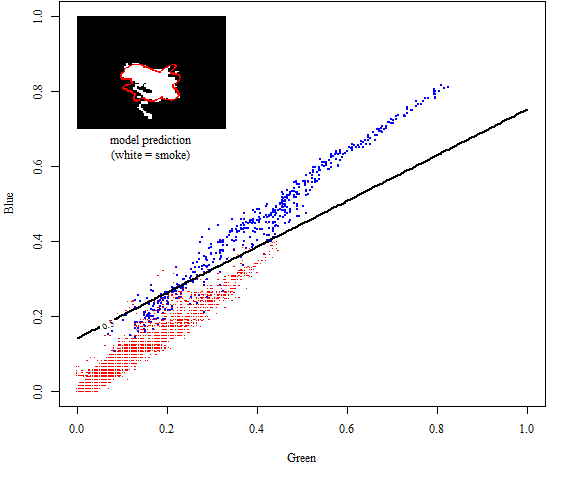
Why is the 0.5 probability contour a straight line? Actually all of the equal-probability contours are straight lines, as a consequence of the model’s form. The logistic model for the present case is
\[\log\left(\frac{\pi_i}{1-\pi_i}\right) = \beta_0 + \beta_1G_i + \beta_2B_i.\]
On any contour line, the probability \(\pi_i\) is a constant value by definition. So on a contour we have
\[\log\left(\frac{\pi_i}{1-\pi_i}\right) = \mathrm{constant} = \beta_0 + \beta_1G_i + \beta_2B_i.\]
In other words, logistic classifiers’ decision boundaries are linear in the feature space. To get a nonlinear decision boundary in the (G,B) plane, we need to add more features that are themselves nonlinear functions of G and B.
Expanding the feature space
The second part of the expository example continues to use only the G and B data, but includes higher-order terms and interactions, for a total of 10 predictors. The model is
\[\begin{eqnarray}\log\left(\frac{\pi_i}{1-\pi_i}\right) & = & \beta_0 + \beta_1G_i + \beta_2B_i + \beta_3G_i^2 + \beta_4B_i^2 + \beta_5G_iB_i\\ & & + \beta_6G_i^3 + \beta_7G_iB_i^2 + \beta_8B_iG_i^2 + \beta_9B_i^3 + \beta_{10}G_i^2B_i^2. \end{eqnarray}\]
This model is constructed and fit using:
fit2 <- glm(class ~ (G + B + I(G^2) + I(B^2))^2 ,
family=binomial(link="logit"), data=dat)
summary(fit2)The fitted model summary is:
Call:
glm(formula = class ~ (G + B + I(G^2) + I(B^2))^2, family = binomial(link = "logit"),
data = dat)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.5548 -0.0399 -0.0087 -0.0018 4.2270
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -15.414 1.422 -10.837 < 2e-16 ***
G -43.155 22.150 -1.948 0.05138 .
B 177.031 22.563 7.846 4.29e-15 ***
I(G^2) -788.447 111.020 -7.102 1.23e-12 ***
I(B^2) -922.575 174.924 -5.274 1.33e-07 ***
G:B 1186.098 272.838 4.347 1.38e-05 ***
G:I(G^2) 1992.547 486.099 4.099 4.15e-05 ***
G:I(B^2) 3431.653 1567.291 2.190 0.02856 *
B:I(G^2) -3971.402 1460.783 -2.719 0.00655 **
B:I(B^2) -491.490 589.582 -0.834 0.40449
I(G^2):I(B^2) -588.066 121.895 -4.824 1.40e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 15322.2 on 24749 degrees of freedom
Residual deviance: 2968.7 on 24739 degrees of freedom
AIC: 2990.7
Number of Fisher Scoring iterations: 11The coefficients of most of the predictors are very large, with large standard errors. This is a consequence of multicollinearity. It does not necessarily mean that the model is inappropriate for prediction purposes, but trying to find meaning in the coefficient values and/or p-values is perilous. See here for more on this and some code for diagnosing collinearity and separability problems.
The code for producing the plot of the decision boundary is ommitted here (though it’s present in example_script.R). It’s the same as the code to produce the previous plot. Here is the figure:
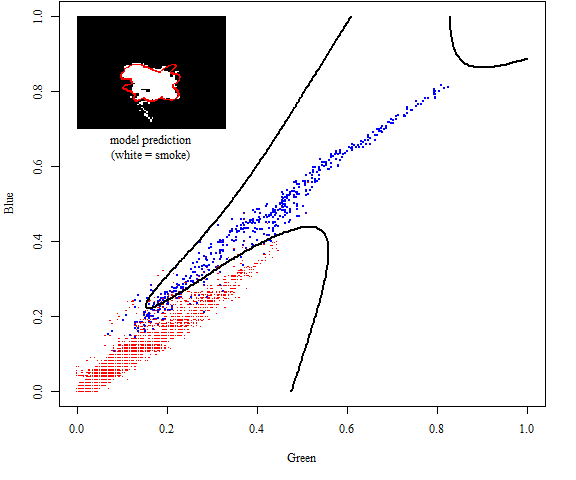
Digression: use of principal components to improve numerical performance
This is a bonus topic put here for those that are interested. It can be skipped without harm.
One way of ameliorating multicollinearity among the predictors is transforming the design matrix into its principal components, and then using only a subset of the principal components. Notes on this approach:
- If we use all of the principal components, we get the same result as if we used the full original design matrix. So no gains to be had that way. Instead we can use the PC approach as a way to reduce numerical difficulties and to make subset selection easier.
- The principal components are orthogonal to each other. When using the PCs as predictors in a linear model this has the advantage that it allows the coefficients to be estimated independently. However this advantage does not carry over to a nonlinear model like a GLM. Model selection with principal components as predictors still requires a model-by-model search, since adding or removing variables can influence all of the coefficient estimates.
- Using principal components as predictors, it is tempting to choose the number of principal components in the standard way, i.e., by using the scree plot or “proportion of variance explained.” However this does not consider the relative value of each PC for prediction of the response, which is what we’re interested in (reference for this point: Jolliffe, 19821).
The example below uses principal components to build a classifier for the same small example case we’ve considered so far. The model is the same as before: G, B, squares, and interactions. The number of principal components is chosen in the simple way: the first \(r\) PCs are taken such that at least 99% of the variance in \(\mathbf{X}\) is explained. Note: I also repeated this analysis using the PCs most correlated with the response, and got better results (not shown).
# Leave out the intercept here, just figuring out the PCs for the covariates
X <- model.matrix(class ~ (G + B + I(G^2) + I(B^2))^2 - 1, data=dat)
S <- cov(X)
p <- dim(S)[1]
eig <- eigen(S)
pve <- eig$values/sum(eig$values) #-Proportion of variance explained
r <- sum(cumsum(pve)<0.99) + 1 #-Choose first r PCs so that at least 99% var expl.
E <- eig$vectors[, 1:r] #-The first r eigenvectors
rownames(E) <- colnames(X) #-Helps interpretation of eigenvectors
A <- X%*%E #-Reduced data matrix
nms <- character(length = 0)
for (i in 1:r) nms <- c(nms, paste("a", i, sep=""))
colnames(A) <- nms
newdf <- cbind(data.frame("class"=dat$class), as.data.frame(A))
r #-Equals 3
head(newdf) #-Look at the new data
#now repeat the fitting.
fit3 <- glm(class ~ ., family=binomial(link="logit"), data=newdf)
summary(fit3)> r #-Equals 3
[1] 3
> head(newdf) #-Look at the new data
class a1 a2 a3
1 0 -0.3533830 0.1708114 0.04795235
2 0 -0.3533830 0.1708114 0.04795235
3 0 -0.3401167 0.1684247 0.04750041
4 0 -0.3401167 0.1684247 0.04750041
5 0 -0.3978829 0.1768675 0.04632803
6 0 -0.3978829 0.1768675 0.04632803
> summary(fit3)
Call:
glm(formula = class ~ ., family = binomial(link = "logit"), data = newdf)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.5090 -0.1089 -0.0628 -0.0427 3.1994
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -7.0963 0.1812 -39.152 < 2e-16 ***
a1 -10.7081 0.2567 -41.716 < 2e-16 ***
a2 7.5565 1.0610 7.122 1.06e-12 ***
a3 -52.0602 1.3468 -38.655 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 15322.2 on 24749 degrees of freedom
Residual deviance: 3551.8 on 24746 degrees of freedom
AIC: 3559.8
Number of Fisher Scoring iterations: 8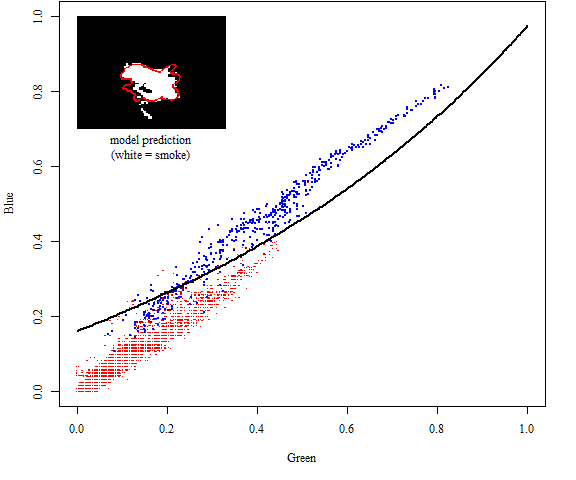
A few thoughts on using PCs:
- It can help things numerically, but it doesn’t seem to offer much in terms of actual improvements in predictive power (at least in this case).
- It potentially provides an escape route to avoid time-consuming model searches with large predictor sets: one could get the principal components, and then take the \(r\) PCs most correlated with the response as the subset of predictors. Then we only need to choose \(r\), rather than doing a model search at each candidate \(r\).
- Of course, if we do the above approach, we could just as well use LASSO or ridge regression too. Can’t say ahead of time which method (subset selection, PCs, LASSO, ridge) would be best.
An Extended Example
The code below uses the full set of pixels from both sub-images, and divides them randomly into three groups: training (50%), validation (25%), and test (25%). In this case we will consider more candidate variables, and include a model selection step. Both genetic algorithm (GA) search and LASSO regularization will be used to do model selection.
I will divide the code into a few chunks; for each chunk the code will be given, followed by some of the ouput and some remarks. I’ll keep the remarks brief, since the comments in the code cover most of the details.
The first chunk involves getting organized and dividing the data into the three groups.
# For this example, we will use all three color channels R, G, B as well as
# their squared terms, square root terms, and all two-way interactions among
# powers of different variables. That gives a total of 36 variables to choose
# from. If we seek the best 6-variable model from this set of predictors, we
# have 1947792 candidate models, which is at least somewhat large.
dat <- RGBdata #-Data to use for this example.
smoke <- dat$class==1 #-For selecting only smoke pixels.
set.seed(1234) #-For reproducibility of sampling.
# Assign pixels randomly into training/validation/test groups with a 50/25/25
# split. For simplicity just do this at random (don't fix the proportion of
# smoke/nonsmoke pixels in each group).
npix <- length(smoke) #-55375 pixels.
pick <- sample(1:npix) #-Assign random numbers 1 to npix to rows of dat.
cutoff1 <- round(0.5*npix) #-Rows with numbers 1 to cutoff1 go to training.
cutoff2 <- round(0.75*npix) #-Rows with numbers cutoff1+1 to cutoff2 go to val.
traindf <- dat[pick<=cutoff1, ]
valdf <- dat[(pick>cutoff1)&(pick<=cutoff2), ]
testdf <- dat[pick>cutoff2, ]
# This method of making the model matrix is clunky but does the job. Write it
# as a function and apply it to the three data frames to get model matrices.
getMM <- function(df){
model.matrix(
class ~ (R + G + B + I(R^2) + I(G^2) + I(B^2)
+ I(R^(1/2)) + I(G^(1/2)) + I(B^(1/2)))^2
- R:I(R^2) - R:I(R^(1/2)) - I(R^2):I(R^(1/2))
- G:I(G^2) - G:I(G^(1/2)) - I(G^2):I(G^(1/2))
- B:I(B^2) - B:I(B^(1/2)) - I(B^2):I(B^(1/2))
, data=df)
}
Xtrain <- getMM(traindf)
Xval <- getMM(valdf)
Xtest <- getMM(testdf)
Ytrain <- traindf$class #-true classes for training set.
Yval <- valdf$class #-true classes for validation set.
Ytest <- testdf$class #-true classes for test set.First we will try model selection using GA. As this is just an example we will only consider selecting models of a single size: six variables. The GA needs an objective function, so we have to define that first. We’ll use the validation-set deviance to select our model. Remember, the training data is used for coefficient estimation, the validation set is used for model selection.
# Use a genetic algorithm (package kofnGA) to search for the best 6-variable
# model. To do this we need an objective function. This objective function
# takes a length-six index vector (the columns of X to use in the model) as
# its first argument, and returns a measure of model quality (validation-set
# deviance) as its result.
# Create the objective function.
ObjFun <- function(v, X1, Y1, X2, Y2){
# v is the vector of columns to use.
# X1 is the model matrix for the training data (all columns, and intercept)
# y1 is the zero/one response vector for the training data
# X2 is the model matrix for the validation data (all columns, and intercept)
# y2 is the zero/one response vector for the validation data
M1 <- X1[, c(1,v+1)] #-Model matrix for the model corresponding to v (train).
M2 <- X2[, c(1,v+1)] #-Model matrix for the model corresp. to v (validation).
# Fit the model on the training data. Keep only the coefficients and
# convergence flag. Note, we use speedglm.wfit (speeglm package) rather than
# glm() or glm.fit() because speeglm is considerably faster, even for this
# "small" problem size. Note: setting tol.solve=0 is a hack to let the search
# continue in case of computationally singular matrices.
fit <- speedglm.wfit(
y=Y1, X=M1, family=binomial(link="logit"), sparse=FALSE,
eigendec=FALSE, tol.solve=0)[c("coefficients","convergence")]
if(!fit$convergence) return(1e20) #-Return bad value if not converged.
# Use the fitted coefficients to get predicted probabilities for the
# validation data. Then compute the deviance (minus 2 times the log-
# likelihood).
eta <- M2 %*% fit$coefficients #-Linear predictor values.
pp <- exp(eta)/(1+exp(eta)) #-Predicted probabilities.
pp[pp==1] <- 1 - .Machine$double.eps #-To avoid -Inf*0 in dev calculation.
dev <- -2*sum(log(pp)*Y2 + log(1-pp)*(1-Y2))
return(dev)
}With ObjFun defined, we can run the GA search. Output follows the code.
# Now do the model search using kofnGA (see that package's documentation for
# more information).
# === WARNING: ===
# this step could take time because of repeated model fitting. Run time is
# roughly proportional to ngen*popsize. As an estimate you could budget
# ngen*popsize/500 minutes for this problem.
# ================
require(kofnGA)
require(speedglm)
GAsearch <- kofnGA(n=36, k=6, OF=ObjFun, ngen=250, popsize=50,
X1=Xtrain, Y1=Ytrain, X2=Xval, Y2=Yval)
summary(GAsearch)
colnames(Xtrain)[GAsearch$bestsol] #-Show the variables chosen.
windows(width=6, height=5)
par(cex=0.75, mar=c(5,4,0,2)+0.1, family="serif")
plot(GAsearch)Genetic algorithm search, 250 generations
Number of unique solutions in the final population: 1
Objective function values:
average minimum
Initial population 5717.950 5335.628
Final population 5282.051 5282.051
Best solution (found at generation 224):
3 8 9 11 13 36
> colnames(Xtrain)[GAsearch$bestsol] #-Show the variables chosen.
[1] "G" "I(R^(1/2))" "I(G^(1/2))" "R:G" "R:I(G^2)"
[6] "I(R^(1/2)):I(B^(1/2))"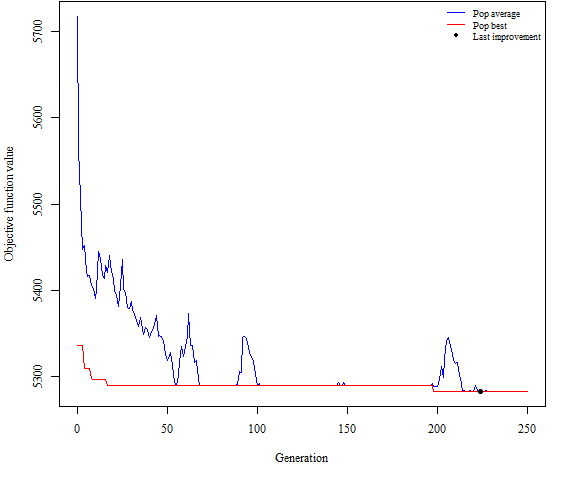
plot(GAsearch).The output shows that model \(G, R^{\frac{1}{2}}, G^{\frac{1}{2}}, RG, RG^{2}, R^{\frac{1}{2}}B^{\frac{1}{2}}\) was selected. Interesting that blue only shows up in one term. We can now evaluate the performance of this model on the test set.
# Finally, take the best model found and inspect the confusion matrix for
# prediction on the test set. This part uses function conf(), found in
# helper_function.R, to create the confusion matrix. The confusion matrix is
# given S3 class ConfusionMatrix, with a summary method.
v <- c(1, GAsearch$bestsol + 1)
M1 <- Xtrain[, v] #-Model matrix for the best model, using training data.
M3 <- Xtest[, v] #-Model matrix for the best model, using test data.
fit <- speedglm.wfit(y=Ytrain, X=M1, family=binomial(link="logit"), sparse=FALSE,
eigendec=FALSE)
eta <- M3 %*% fit$coefficients #-Linear predictor values.
pp <- exp(eta)/(1+exp(eta)) #-Predicted probabilities.
prd <- pp>0.5 #-Test-pixel predictions.
CM <- conf(prd,Ytest)
summary(CM)> summary(CM)
Confusion matrix:
predicted
true 0 1 total
0 0.69149090 0.0403785 0.7318694
1 0.03936723 0.2287634 0.2681306
total 0.73085813 0.2691419 1.0000000
Overall error rate:
[1] 0.07974574
Classwise error rates:
class 0 class 1 average
0.05517173 0.14682112 0.10099643 The overall error rate was about 8%, with lower classwise error rate on class 0 (nonsmoke, 5.5%) than on class 1 (smoke, 14.7%).
An alternative approach to model selection is to use LASSO. This is done using the following code.
# First use the glmnet package to get the family of LASSO-regularized models.
# A sequence of models is fit with different values of the regularization
# parameter lambda.
require(glmnet)
fit2 <- glmnet(Xtrain, Ytrain, family="binomial")
# Now, choose the value of lambda that minimizes validation-set deviance. The
# fitted coefficients with this lambda value define the best model found by this
# method
valdev <- function(p) -2*sum(log(p)*Yval + log(1-p)*(1-Yval)) #-val set deviance
lams <- fit2$lambda #-The sequence of lambda values.
deviances <- numeric(length=length(lams))
for(i in 1:length(lams)){
p <- predict(fit2, newx=Xval, s=lams[i], type="response")
deviances[i] <- valdev(p)
}
bestloc <- which(deviances==min(deviances, na.rm=TRUE))
bestlam <- lams[bestloc]
bestbeta <- fit2$beta[ , bestloc] #-Returns all coeffs, even zeroed ones...
bestbeta[bestbeta!=0] #-Display the selected variables and their coefficients.> bestbeta[bestbeta!=0] #-Display the selected variables and their coefficients.
R I(G^2) I(B^2) I(R^(1/2)) I(G^(1/2))
-2.756217e+01 4.098836e+01 -1.662455e+02 -1.944852e+01 -6.182804e+00
I(B^(1/2)) G:B G:I(R^2) G:I(B^(1/2)) B:I(R^(1/2))
9.112940e+01 1.033892e+01 -1.244126e+02 8.941487e+01 -4.791525e+00
I(R^2):I(B^2) I(R^2):I(G^(1/2)) I(G^2):I(B^2) I(R^(1/2)):I(B^(1/2))
1.685050e+02 -1.586188e+01 8.113575e+01 -2.993225e-03 The LASSO approach selects a model with 14 variables. How is its performance on the test data?
# And get the predictions on the test pixels. Show confusion matrix.
pp2 <- predict(fit2, newx=Xtest, s=bestlam, type="response")
prd2 <- pp2>0.5
CM2 <- conf(prd2,Ytest)
summary(CM2)> summary(CM2)
Confusion matrix:
predicted
true 0 1 total
0 0.69264663 0.03922277 0.7318694
1 0.04001734 0.22811326 0.2681306
total 0.73266397 0.26733603 1.0000000
Overall error rate:
[1] 0.0792401
Classwise error rates:
class 0 class 1 average
0.05359258 0.14924569 0.10141913 The error rates are almost identical to those of the 6-variable model chosen by GA. Although it chooses a larger model, LASSO has the advantage of computational speed and (because it is a regularization method) reduced concerns about collinearity and numerical instability.
Final Remarks
The preceding extended example included all of the elements of the analysis in the book chapter, but using a pixel count small enough for everything to proceed smoothly. Unfortunately, when scaling the analysis up from a single small image to a collection of megapixel-size hyperspectral images, a variety of practical challenges arise. Here are a few comments on those challenges, for those that might want to try such an analysis on a real-world problem. They are organized in two groups:
It is not possible/practical to hold all of the images in memory simultaneously, so a variety of supporting code is needed to manage the data. For example:
- Functions for loading particular images, converting them from the format they’re stored in to a data frame.
- Functions for sampling pixels in the specified manner from a collection of images on disk.
- Functions for handling images and their true-label masks, allowing for calculation of prediction accuracy measures and creation of visual displays.
Some of this functionality could be obtained from existing packages (the
rasterpackage, for example), but in any case one will have to plan ahead how images will be stored and manipulated.When conducting logistic regression analyses (actually, any matrix operations) on large data sets, memory usage becomes critical and the standard “go-to” packages might not work as you expect. We observed the following:
- As mentioned above, special “big data” packages like
speedglmworked much better than the usualglm. - For LASSO predictions, the
predict()method choked on the large data set. I had to write my own prediction function taking the coefficients from the fittedglmnetobject. - In the analysis of the chapter the data set had 100 thousand rows and 36 main effects. The largest feature space we considered had several thousand columns. Model selection by GA involves repeatedly taking subsets of these columns, but because of their number it was not possible to pre-compute all of them and hold them in memory. Instead, the objective function had to construct the model matrix corresponding to a given solution on the fly as needed. This is not straightforward to implement.
- As mentioned above, special “big data” packages like
While we had to handle all of these challenges as a part of our study, I have not provided the code related to that part of the analysis. It is not polished enough for distribution. If there is interest, however, the possibility remains to tidy it all up and put it together in a package that would facilitate this sort of analysis. Any feedback or suggestions are welcome.